Have you ever wondered how your maths teacher can tell you instantly the answer to $7.5^2 = 56.25$. Do check it. It is quite likely they are using a little trick which is very easy to use and almost as easy to prove.
The technique is as follows:
You can apply this to any "something and a half, squared" problem.
Example $8.5^2$. $8 \times 9 + 0.25 = 72.25$.
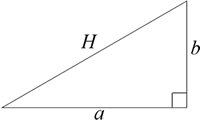
Pythagoras Theorem states that the square on the hypotenuse in a right angled triangle is equal in area to the sum of the squares on the other two sides. \[H^2 = a^{2} + b^{2} \]
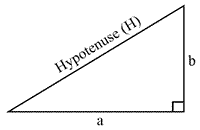

Alternatively, referencing the pink image, the theorem can be defined as
\[\sin^2{\theta}+\cos^2{\theta} \equiv 1\]The square root of a number is a number which, when multiplied by itself (squared), gives you the number you started with. It is the opposite of squaring.
A square root is shown by placing a tick before the number or expression. $\sqrt{36} = \pm6$
For example, $\sqrt{9} = \pm 3$. Please note that there are always two square roots of a number. They are the same size but with opposite signs. Hence the plus or minus symbol.
Differentiation is a mathematical technique concerned with finding the gradient of a line or curve at a point.
The derivative of a function is the result of doing differentiation to a function.
The notation for a derivative is either $f'(x)$ which is the function notation or $\frac{dy}{dx}$ which is the most common notation in the early stages of Calculus.
Isaac Newton was one of the greatest mathematical minds of all time. He was also petty and vindictive and spent a great deal of time trying to destroy those he saw as rivals (Robert Hook, Gottfried Leibniz...) and attempting (and failing) to make a success of alchemy.
There is a lesson here for all of us. People who are imensely talented in one area of life, can be total failures in other areas and all of us humans are to a greater or lesser extent, prey to this syndrome.
Newton was one of the inventors of the calculus and formulated his three laws of motion, which are still used to this day.
The gradient of a line is the quotient of the change in the $y$-coordinates divided by the change in the $x$-coordinates.
\[\text{Gradient } = \frac{\text{Change in }y}{\text{Change in }x}\]Division is the operation where we split up a group of things into smaller groups of the same size.
$18 \div 3 = 6$ is a division problem, involving a dividend ($18$) divided ($\div$) by a divisor ($3$) giving a quotient ($6$).
\[\text{Quotient } = \frac{\text{Dividend}}{\text{Divisor}}\]A difference is the result of a subtraction problem
eg. The difference between $3$ and $9$ is $6$ or $9 - 3 = 6$
eg. The difference between $3$ and $-2$ is $5$ or $3 - (-2) = 5$
A sum is the result of a addition problem
eg. The sum of $4$ and $7$ is $11$ or $4 + 7 = 11$
eg. The sum of $3$ and $-2$ is $1$ or $3 + (-2) = 1$
A product is the result of a multiplication problem
eg. The product of $3$ and $9$ is $27$ or $3 \times 9 = 27$
eg. The product of $3$ and $-2$ is $-6$ or $3 \times (-2) = -6$
The result of a division problem
eg. The quotient of $12$ and $4$ is $3$.
Or mathematically, $12 \div 4 =3$.
The process of finding the sum of two or more quantities. Addition is the simplest arithmetic operator, represented by the symbol $+$.
\[3+5=8\]The process of finding the difference between two quantities. Subtraction is represented by the symbol $-$.
\[12-4=8\]Multiplication is a shorthand notation in arithmetic, to avoid lengthy addition problems. For example, $3+3+3+3+3+3+3+3$ can be written as $3 \times 8$, which tells us that $8$ $3$s are to be added together. As the numbers involved get bigger, the shorthand becomes more and more useful.
$3 \times 8 = 24$
A Power is a small number written at the top and right of another number to show the numnber of times the base number is to be multiplied by itself (eg. $3^4 = 3 \times 3 \times 3 \times 3 = 81$) the power in this example is $4$, while the base is $3$.
The Natural numbers are the counting numbers. The positive whole numbers. The first Natural number is 1 and there are an infinite number of them.
$ 3 \in\Bbb{N}$
3 is a member of the set of Natural numbers
Integers are all of the counting numbers ($\Bbb{N} = \Bbb{Z}^+$) as well as the negative whole numbers ($\Bbb{Z}$-) and zero ($0$). So any whole number on the real number line, positive or negative or zero, is an integer.
$\{-4, -3, -2, -1, 0, 1, 2, 3, 4\} \in \Bbb{Z}$Rational numbers are any numbers which can be written as a fraction or one integer divided by another.
Real numbers are those which fill up the number line completely, with no gaps at all. They include all of the natural, integer, rational & irrational numbers.
Complex numbers are the outermost set of numbers. In other words, every single number anyone can name is a complex number.
The complex numbers are a 2-dimensional representation of the most general numbers we can work with in mathematics. They seem a bit silly when you first meet them and it took quite a few centuries before they were accepted by the wider mathematical community. However, they are very useful in all sorts of modelling in design, electronics and many more.
Complex numbers are made up from a real part and an imaginary part, which are written as a simple sum, like $a + ib$ where $i = \sqrt{-1}$ and $a, b$ are real numbers.
\[\begin{aligned}[t] & \ (1-i)(1+i) \\ = \ &1+i-i-i^2\\ = \ & 1+1\\ = \ & 2\\ \hline \end{aligned}\]
An irrational number is one which cannot be written as a fraction (integer $\div$ integer).
$\sqrt{2}$ is irrational.
$\pi$ is irrational
Numbers which are greater than zero. A positive number $>0$.
Negative numbers are any numbers which exist on the number line, and inhabit the region to the left of zero.
They are extremely useful when considering concepts like debt in Economics, height below sea level in Geography, and similar ideas.
The number which represents nothing. $0$. Zero arrived on the scene very late compared to most whole numbers. It's first known use is in the 6th century CE India.
Ancient mathematicians could not see how you can use a word or symbol to represent something which by definition, isn't there.
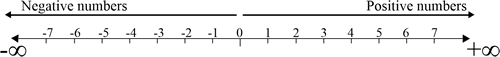
A fraction is a number form which shows many of the numbers in between whole numbers, though by no means all of them. It takes the form of an integer (whole number) divided by another integer.
It is fine to consider a fraction as being another way of showing a division operation.
\[2 \div 3 \text{ means the same as } \frac{2}{3}\]Imaginary numbers ($\mathbb{C}$) are numbers based around multiples of $i$, where $i=\sqrt{-1}$.
\[\sqrt{-9} = \sqrt{9} \times \sqrt{-1} = 3i\]In this calculation, $3i$ is an imaginary number.
Imaginary numbers cannot exist on the real number line, so imaginary numbers are shown on a vertical axis at $90^\circ$ to the real number line.
Directed number is a term used to describe integers (mostly). In other words, directed numbers are numbers where some direction is implied. This becomes important in navigation: the journey outward is the opposite of the journey back again, even though it covers the same ground, we can consider one as positive and the other negative.
It is very important to work carefully when using operations on directed numbers. It is my recommendation when working with directed numbers, that you use implied multiplication with brackets rather than using the $\times$ sign. This is to avoid statements such as $4 \times -3 = -12$ where you have a $\times$ and a $+$ next to each other, as this can lead to confusion. Here is the bracketed alternative: $4\big(-3 \big) = -12$, which means the same thing though, to my mind, it is clearer.
An expression is the mathematical equivalent of a phrase or clause in standard language. It is not usually a complete sentence unless it is part of an equation or inequality. The simplest expression would be a term, which can be a number ($3$) or letter representing a number ($x$), or a combination of the two like $2x$.
More complex expressions, like $2x^3 - 3x^2 + 4x -5$ can be made up from several terms connected with operators ($+ - \times \div$).
Q: If an apple costs $t$ pence, how much do 20 apples cost?
A: $20t$ pence.
Q: Simplify $x +2x +4x$
A: $7x$
An equation is a mathematical sentence. It is a way of showing that one expression is equal to another expression.
An equation should be thought of as a balance. The two sides of the equation must always be equal, so when we are manipulating equations, it is essential that we perform the same (allowable) operations to both sides of the equals sign.
Here are 2 equations. Note that there is always an expression either side of an equals sign.
$2x+3=11$
$x^2 - x -6=0$
This is the number being divided by. In the expression $20 \div 5$, $5$ is the divisor.
In the identity, $20 \div 5 = 4$, $5$ is the divisor, $20$ is the dividend and $4$ is the quotient.
This is the number being divided up. In the expression $20 \div 5$, $20$ is the dividend.
In English, a dividend is the surplus profit of a company, which is divided up after a year of profitable exploitation of its workforce.
In mathematics, it means roughly the same thing, minus the exploitation. A dividend is the number being divided up.
In the identity $10 \div 2 = 5$, the dividend is 10.
BIDMAS is an acrostic, where each letter refers to the operations in the order they should be carried out.
Brackets
Indices
Division
Multiplication
Addition
Subtraction
There are many variants of this. The first I learned was BODMAS (the O stood for Order, which means the same as index, power or exponent. However, it is only really used in higher level mathematics, these days, where we talk about the order of a polynomial.)
BOMDAS works as well (the M and the D being reversed, makes no difference at all, mathematically.) This also has the advantage of sounding very funny. It generally gets a laugh in class.
$\begin{aligned}[t] &(6+3) \times 4 - 2\\ =&9 \times 4 - 2\\ =&36-2\\ =&34 \end{aligned}$Brackets are used in mathematics, to make otherwise ambiguous expressions, more obvious in their meaning. In addition, they can be used to change the meaning of an expression.
eg. The following expression correctly gives the answer as $14$, $2 + 3 \times 4 = 14$, because according to BIDMAS, the multiplication must be performed before the addition. However, if we insert brackets around the $2+3$, this changes the value as follows: $(2+3) \times 4 = 20$, as now, the bracket must be evaluated first.
Of always means the same as $\times$. In mathematics it is a synonym for multiplication. Think of it as being short for lots of.
$2 \text{ lots of } 3 = 6$
$\frac{1}{4} \text{ of } 20 = 5$.
The main four operators are $ \ \ \ + \ \ \ - \ \ \ \times \ \ \ \div$
These represent, in order, Addition, Subtraction, Multiplication and Division.
These are binary operators, which means that they go between a pair of numbers or expressions.
iff means If and only if. Just a bit stronger than an ordinary if.
The symbol for iff is $\iff$.
A set of numbers have a product of $0$, iff one or more of the set of numbers is $0$.
To change the subject of a formula to a specified variable
An identity is a congruent relationship in algebra. It is always true whatever the value(s) of the variable(s). For example
\[\begin{aligned}[t] &\sin^2{x}+\cos^2{x} \equiv 1\\ \text{or }&\\ &2(x+1) \equiv 2x+2 \end{aligned}\]You should note that these statement are true, $\forall$ (for all values of) $x$.
It is denoted by a special equals symbol with an extra bar ($\equiv$).
For all values of a variable.
The function $f$ is defined as $f(x)=\sqrt{x}, \ \forall x \in \mathbb{R}^+$
Geometry is the mathematics of physical space. It is initially the study of lines, 2-D shapes & later 3-D shapes, trigonometry and all sorts of other goodies.
Isosceles is a word to describe a triangle with two equal lengths and two equal angles.

The following acrostic may be helpful in learning how to spell isosceles.
I Sit On Sand Carefully Eating Little Egg Sandwiches

Supplementary angles are a pair of angles which add up to $180^\circ$. Examples of supplementary angles are:
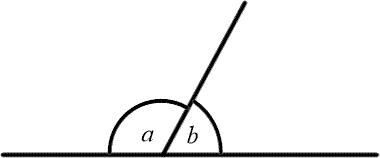

Supplementary angles add up to $180^\circ$.
Angles at a point produce a full revolution, which is $360^\circ$.
Angles at a point add up to $360^\circ$.

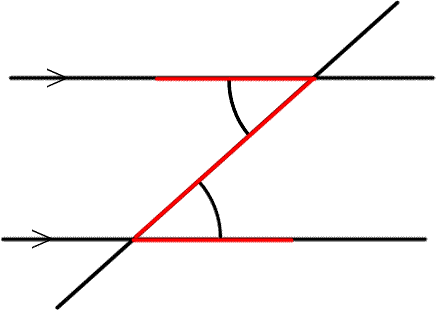
Angles in a Z shape between parallel lines are called alternate angles. They are the equal.


An equilateral triangle is one whose sides are all the same length. The angles in an equilateral triangle are also the same, so each of them is $180 \div 3 = 60^\circ$.
Equilateral triangles have 3 lines of symmetry and rotational symmetry of order $3$.
A quadrilateral is a closed, 4 sided plane figure. Squares, rectangles, parallelograms, rhombi & trapezia are all quadrilaterals.
A rectangle is a parallelogram all of whose angles are $90^\circ$, hence the name rectangle.
Most doors (unless you are a Hobbit) are rectangular.
A trapezium (plural: trapezia) is a quadrilateral (4 sided figure) with one pair of parallel sides.
A parallelogram is a quadrilateral with $2$ pairs of parallel sides. Each pair of parallel sides are equal in length
Adjacent angles in a parallelogram add up to $180^\circ$.
Opposite angles in a parallelogram are equal.
The diagonals of a parallelogram, bisect one another.
A rhombus (plural rhombi) is a parallelogram, all of whose sides are of equal length.
A diamond shape (in a pack of cards) is a rhombus.
Polygon is a Greek word, which literally translates to "Many angles". Poly means many and gon means an angle.
Polygons are closed shapes with straight sides.
Corresponding angles are equal. These are angles which sit in the same position between parallel lines. They are sometimes called F - angles.
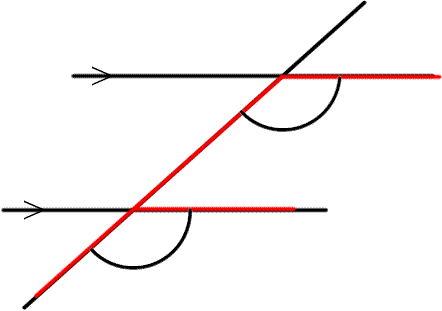
Co-interior or Allied angles are supplmentary. That is they add up to $180^\circ$.
One way of thinking about co-interior angles is that they are adjacent (next to) angles in any parallelogram. They are sometimes called C - angles.

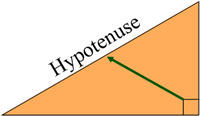
The longest side in a right angled triangle. It is the side which is opposite the right angle $(90^{\circ})$.
The opposite side in a right triangle is the side which sits opposite the angle you are referencing.

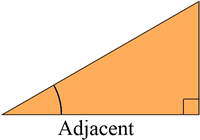
The adjacent side in a right angled triangle is the side next to the angle you are referencing, that isn't the hypotenuse.
A closed (the start of the path connects to the end of the path) $3$ sided plane figure.
The sum of the interior angles of a triangle is always $180^{\circ}$.
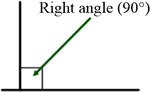
A right angle is a quarter of a full turn. In degrees, it is $90^{\circ}$. In radians, it is $\frac{\pi}{2}$
A right triangle or right angle triangle is a triangle which contains a $90^{\circ}$ angle, with the other $90^{\circ}$ inside the triangle shared between the other two angles.
Little is known about Pythagoras (c. 570 - c. 495 BCE) as no writings of his remain. He born on the island of Samos. He had some very ideas, especially regarding beans which were reputedly forbidden in his commune.
His school of thought (the Pythagoreans) was responsible for the famous theorem about right angle triangles, $H^{2} = a^{2} + b^{2}$.
Pythagoras also made discoveries in Music where he pioneered the connection between mathematics and musical scales.
He was also one of those (along with the contemporary philosopher, Parmenides) who realised that the Earth is a globe and not flat and also was among the first people to realise that the Morning star (as opposed to the splendid newspaper, The Morning Star) and the Evening star were in fact the same object, later called Venus.
An equivalent fraction is a fraction which uses different symbols to represent fractions of the same size. In English, we say that "two quarters" is the same as "one half". This is equivalence. In mathematical notation, we can say that \[\frac{2}{4} = \frac{1}{2}\] This is true, as can be demonstrated by showing both as division problems $2 \div 4 = 0.5$ and $ 1 \div 2 = 0.5$.
A numerator is the number written above the line in a fraction. This tells us how many of the fractional parts we have.
eg $\frac{2}{5}$ has a numerator of $2$.
It derives from the Latin word numerus meaning a number
A denominator is the number written below the line in a fraction. This tells us what type of fraction we are dealing with.
eg $\frac{2}{5}$ has a denominator of $5$.
It derives from the Latin word nomine meaning a name
Mixed numbers are, as their name suggests, a mixture of whole numbers and fractions. For example $2\frac{1}{2}$.
Sometimes called improper fractions, top-heavy fractions are situations where the numerator is bigger than the denominator.
For example $\frac{7}{3}$.
A remainder occurs when a division problem does not compute to a whole number.
For example, in the calculation, $7 \div 3$ we can see that the whole number part of the answer will be $2$ but with $1$ left over. So $7 \div 3 = 2 \text{ remainder } 1$
The reciprocal of a number is the number which multiplies by a given number to give $1$.
For example $5 \times 0.2 = 1$, so the reciprocal of $5$ is $0.2$, and vice-versa.
It is quite possible to find a reciprocal in decimal form, but it is substantially easier when the number is written as a fraction.
Once you have written the number as a fraction, the reciprocal is the fraction turned upside down.
For example, the reciprocal of $\frac{12}{17}$ is $\frac{17}{12}$.
A square is the result of multiplying a number by itself. $4^2 = 4 \times 4 = 16$.
It can also mean a plane quadrilateral with four equal sides and four $90^\circ$ angles.
A square is a rhombus whose angles are all $90^\circ$. Alternatively, it could be defined as a rectangle, all of whose sides are equal.
All squares are rhombi.
Not all rhombi are squares.
In a group of numbers the HCF is the biggest number which is a factor of every number in the group.
It is often referred to as the GCD (Greatest Common Divisor).
eg. $HCF(6, 8) = 2$.
In a group of numbers the LCM is the smallest number which is a multiple of every number in the group.
eg. $LCM(6, 8) = 24$.
A prime number is one that has precisely $2$ factors, the number itself and $1$.
$2$ is therefore the first and the only even prime number.
A percentage is shorthand for a fraction out of $100$, whose denominator is $100$.
For example $43\% = \frac{43}{100}$
Ratio is a way to compare the relative size of numbers. It is the number of times a number contains another. Ratios can be cancelled down like fractions.
For example, if there are $10$ bananas and $8$ apples in a fruit bowl, then the ratio of bananas to apples is $10:8$, which can be cancelled down to $5:4$.
Chomolungma is the Tibetan name for the highest mountain on Earth. It is often called Mount Everest in the West, perhaps after the double glazing company. :)
It is approximately 8 850 m (29 030 ft) high.
Reimann, (1826 - 1866) was a German mathematician who made considerable advances in (mainly) Analysis and Number theory, following on from mathematical giants Gauss and Euler. He laid much of the mathematical groundwork for Einstein's theory of General Relativity, but is most widely known for an unproven hypothesis, which is simply called the "Riemann Hypothesis", which concerns the zeros (solutions) of zeta functions. It states that "The real part of every non-trivial zero of the zeta function is $\frac{1}{2}$.
This doesn't sound like much, but for maths people, it is a very big deal.
This conjecture, which is an analog for the incidence of prime numbers on the number line, is one of the most famous unproven problems in mathematics and number theory. A great deal of mathematics which has been postulated since Riemann's time depends on the hypothesis. If it were to be shown to be false, all of this work will have to be rethought.
Every non-prime natural number $(\Bbb{N})$, can be written as a unique product of prime numbers.
For example, \[12 = 2 \times 2 \times 3 = 2^2 \times 3\]
These are logarithms to the base of $e = 2.718281828459045...$. $e$ occurs in nature all over the place and becomes fundamental to our understanding of advanced mathematics.
A logarithm (log) is another word for a power, index or exponent. The difference with logs is not their meaning but the notation which accompanies them, which can be confusing.
Consider the following identity $3^5 = 243$. The $3$ is the base, $5$ is the logarithm, $243$ is the number. If we consider that the power is the logarithm, then the logarithm notation goes like this: \[5=\log_{3}\left(243\right)\] You can read this as "$5$ is the logarithm, base $3$ of the number $243$".
A differential equation is any equation which contains a term denoting a rate of change. For example \[\frac{dy}{dx} = 2x\] Some differential equations are disguised to look like ordinary ones. For example the constant acceleration formula $v=u+at$ where $u, \ a$ are constants, $v$ is the dependent velocity variable and $t$ is the independent time variable. If we were to write this in its most basic form, it would look like this $\frac{ds}{dt}=u+at$, where $\frac{ds}{dt}$ is the rate of change of $s$, the displacement variable.
Integration is the name we give to a bunch of algebraic and numerical techniques to find the area under graphs. It is also the inverse of differentiation, so it can be used to find a function when we know a connection based on the rate of change of the function we want to find.
DOTS stands for Difference Of Two Squares.
Eg. $a^2-b^2 = (a-b)(a+b)$
This is a useful technique for splitting a complicated fraction into several simple and easily integrable fractions.
Eg. \[\frac{2}{(x-1)(x+1)} \equiv \frac{1}{x-1} - \frac{1}{x+1}\]
The Power Rule in differentiation and integration is the relationship between a polynomial function and its derivative. In words it goes Multiply the power by the coefficient and then reduce the power by 1
.
Symbolically, it looks like this:
\[\begin{aligned}[t] y&=ax^n\\ \frac{dy}{dx}&=anx^{n-1} \end{aligned}\]An even function is defined mathematically as any function where function values of positives and negatives are the same.
\[f(-x) = f(x)\]Practically, an even function is easy to spot, given that it always has refectional symmetry in the $y$-axis.
Examples include $y=\cos{x}$ and $y=x^2$.
An odd function is defined mathematically as any function where function values of positives and negatives have the opposite sign.
\[f(-x) = -f(x)\]Practically, an odd function is easy to spot, given that it always has rotational symmetry order $2$ about the origin $(0,0)$.
Examples include $y=\sin{x}$ and $y=x^3$.
The sine function (written as $\sin$ but pronounced sine) is the length of the opposite side of a right angled triangle whose hypotenuse has length $1$.
In a general right triangle
\[\sin{\theta} = \frac{\text{Opposite}}{\text{Hypotenuse}}\]The cosine function (written as $\cos$ and pronounced koz) is the length of the adjacent side of a right angled triangle whose hypotenuse has length $1$.
In a general right triangle
\[\sin{\theta} = \frac{\text{Opposite}}{\text{Hypotenuse}}\]The tangent function (written as $\tan$ and pronounced tan) is the length of the opposite side of a right angled triangle whose adjacent side has length $1$.
In a general right triangle
\[\tan{\theta} = \frac{\text{Opposite}}{\text{Adjacent}}\]The ubiquity of a thing means something which turns up often in lots of different contexts. The property of seeming to appear everywhere; to be extremely common.
The conjugate of a binomial like $(a+b)$ is the same expression with the sign in the middle toggled between $+$ and $-$.
Examples:
The conjugate of $a+b$ is $a-b$
The conjugate of $3-\sqrt{5}$ is $3+\sqrt{5}$
The conjugate of $x+iy$ is $x-iy$.
Degrees are a measurement of angle. The full revolution is divided into $360$ equal divisions, each of which is a degree. It is thought that the ancient Babylonians used $360$ because it was close to the number of days in a year.
Degrees are further divided into minutes and seconds, to give higher levels of accuracy. There are $60$ seconds in a minute and $60$ minutes in a degree.
Radians are a measurement of angle. The full revolution is divided into $2\pi$ equal divisions, each of which is a radian. The radian, also called circular measure, is a natural (as opposed to artificial) measurement for angle and is used almost exclusively in higher level mathematics.
Radian measure is particularly important once you get onto calculus of trigonometric functions, as it makes those calculations considerably easier to deal with. For more details, please look at the Radians topic, where we discuss this in greater depth.
Gradians were an attempt to decimalise the angle. There are $100$ gradians in a right angle, so $400$ in a full revolution. Gradians are used by Geographers and Surveyors, but they hold little interest for mathematicians.
An even function is one where $f(-x)=f(x)$. Visually, an even function has a line of symmetry in the $y$-axis.
$y=x^{2n} \hspace{10px} n \in \Bbb{N}$, $y=\cos{x}$, $y=\text{cosh}x$ and many others are even functions.
An odd function is one where $f(-x)=-f(x)$. Visually, an odd function has a line of symmetry in the $y$-axis.
$y=x^{2n+1} \hspace{10px} n \in \Bbb{N}$, $y=\sin{x}$, $y=\sinh{x}$ and many others are odd functions.
These formulas give us expansions of sums of angles, in terms of the trig functions of each individual angles. Here are the three standard formulas. They should be learnt by heart. \[\begin{aligned}[t] \sin{(\alpha \pm \beta)} &\equiv \sin{\alpha}\cos{\beta} \pm \sin{\beta}\cos{\alpha}\\ \cos{(\alpha \pm \beta)} &\equiv \cos{\alpha}\cos{\beta} \mp \sin{\alpha}\sin{\beta}\\ \tan{(\alpha \pm \beta)} &\equiv \frac{\tan{\alpha} \pm \tan{\beta}}{1 \mp \tan{\alpha}\tan{\beta}} \end{aligned}\]
These formulas give us expansions of double angles, in terms of the trig functions of the single angle. Here are the three standard formulas. They should be learnt by heart. \[\begin{aligned}[t] \sin{(2\theta)} &\equiv 2\sin{\theta}\cos{\theta}\\ \\ \cos{(2\theta)} &\equiv \cos^2{\theta} - \sin^2{\theta}\\ &\equiv 2\cos^2{\theta} - 1\\ &\equiv 1-2\sin^2{\theta}\\ \\ \tan{(2\theta)} &\equiv\frac{2\tan{\theta}}{1-\tan^2{\theta}} \end{aligned}\]
Increasing means "going up" or "rising" in size, so an increasing function is one with a positive gradient. This means that looking at the graph from left to right, we are going uphill.
Maximum and minimum points are those where a function switches between increasing and decreasing.
Decreasing means "going down" or "descending" in size, so a decreasing function is one with a negative gradient. This means that looking at the graph from left to right, we are going downhill.
Maximum and minimum points are those where a function switches between increasing and decreasing.
These are useful shortcut calculating devices which can be helpful in topics where remembering one little triangle, for example

The disadvantage of these things is that they are not great for understanding what is going on, even though they are very quick and handy.
Irrational numbers (cannot be written as a common fraction) like $\pi \approx 3.14...$ and $e \approx 2.718...$ are used as algebraic constants by using the letters.
Often we need to use irrational numbers like $\sqrt{2} \approx 1.414...$ . The decimal format is inconvenient, difficult to remember and regardless of how many decimal places you use, it will always be an approximation. So instead, we use the square root form in our calculations $(\sqrt{2})$. This is called surd form.
Surd form is not just confined to square roots and can be extended to cube, fourth etc. roots as well, though you will probably only meet them beyond school level mathematics..
Pascal's Triangle is a triangle of numbers where each number in the array is the sum of the two numbers above it. The triangle gives us the coefficients of the expansions of successive powers of $(x+1)$.
It has far too many interesting features to list here. But here are two simple ones:
Here are the first few lines of the triangle which, in reality, continues forever.
\[\begin{array}[c] &&&&&&&&1\\ &&&&&&1 && 1\\ &&&&&1 && 2 && 1\\ &&&&1 && 3 && 3 && 1\\ &&&1&&4&&6&&4&&1\\ &&1&&5&&10&&10&&5&&1\\ &1&&6&&15&&20&&15&&6&&1 \end{array}\]A coefficient is a constant multiplied by a variable expression. So here are some examples:
Substituting into the Maclaurin series, gives
\[e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+..+\frac{x^n}{n!}\]This is a demonstration of how to derive Maclaurin's therem. We can use this series to find approximate polynomial functions for many common functions like $\sin{x}$, $\cos{x}$, $e^x$ etc.
\[\begin{aligned}[t] f(x)&=a_0+a_1x+a_2x^2+a_3x^3+a_4x^4+...\\ f(0)&=a_0 \Rightarrow a_0=f(0)\\ f'(x)&=a_1+2a_2x+3a_3x^2+4a_4x^3+...\\ f'(0)&=a_1 \ \Rightarrow a_1=f'(0)\\ f''(x)&=2a_2+3.2a_3x+4.3a_4x^2+...\\ f''(0)&=2a_2 \ \Rightarrow a_2=\frac{f''(0)}{2!}\\ f'''(x)&=3.2a_3+4.3.2a_4x+...\\ f'''(0)&=3.2a_3 \ \Rightarrow a_3=\frac{f'''(0)}{3!}\\ f^{\mathrm{iv}}(x)&=4.3.2.a_4+...\\ f^{\mathrm{iv}}(0)&=4.3.2a_4 \ \Rightarrow a_4=\frac{f^{\mathrm{iv}}(0)}{4!}\\ \end{aligned}\]Substituting the values of the constants back into our original general polynomial gives
\[\begin{aligned}f(x)=f(0)&+f'(0)x+ \frac{f''(0)x^2}{2!}+\frac{f'''(0)x^3}{3!}\\ +&\frac{f^{\mathrm{iv}}(0)x^4}{4!}+...+\frac{f^{\mathrm{n}}(0)x^{n}}{n!}+...\end{aligned}\]Substituting into Maclaurin's theorem, gives
\[\sin{x}=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+...\]Substituting into Maclaurin's theorem, gives
\[\cos{x}=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+...\]A series is a collection of terms separated by $+$ signs.
eg 1. $1+2+3+4+5+...$
eg 2. $x+x^2+x^3+x^4+x^5+...$
A sequence is a collection of terms separated by commas.
eg 1. $1, \ 2, \ 3, \ 4, \ 5,...$
eg 2. $x, \ x^2, \ x^3, \ x^4, \ x^5...$
To mathematicians, the word complex means made up from multiple parts
, so it is not a synonym for complicated. Complex things can be complicated, but not always.
Complex numbers are numbers which are made up from two parts, the real bit and the imaginary bit, giving us 2D numbers which is very cool indeed.
Heuristic is a lovely word which means "a technique of problem solving, which may not be optimal, but often helps to solve things quicker than otherwise.". But it is much quicker to write down.
Examples include:
Co-linear means that the points mentioned lie on the same straight line.
Bisect means to cut something (a line segment or angle) into 2 equal parts. Literally, to cut in two.
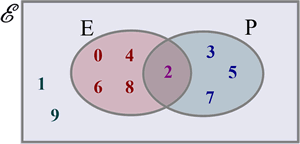
The Universal set is a term in Set theory which defines all of the elements in all the subsets which we are considering. For example if we are considering only prime numbers, then the universal set will be the set of all primes; we do not need to concern ourselves with any numbers which are multiples of another number. Likewise we can define a universal set which is all positive whole numbers, so any fractiions, decimals, negative numbers etc. can be ignored.
It is defined in a Venn Diagram using an enclosing rectangle, with all the sets being inside the universal rectangle.
The universal set is most commonly denoted using a curly E, like this: $\mathscr{E}$.
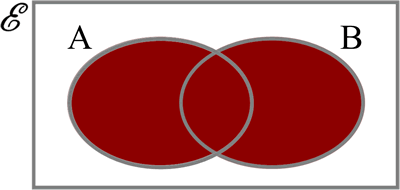
Union is used in set theory to describe an OR relationship. The notation for union is $\cup$. For example $A \cup B = A \text{ OR } B$. In a Venn diagram, the union of 2 sets is all the elements in each of the sets and both.
In logic, Union/OR is an addition.
Intersection is used in set theory to describe an AND relationship. The notation for intersection is $\cap$. For example $A \cap B = A \text{ AND } B$. That is the elements in both sets. In a Venn diagram, the intersection between 2 sets is the overlap between the sets' ellipses.
In logic, Intersection/AND is a multiplication.

Subset is used in set theory to describe a set which is entirely enclosed inside another set. The notation for subset is $\subset$. For example $A \subset B = B \text{ is a subset of } B$. In a Venn diagram, a subset is an ellipse inside its parent ellipse.

Complement is used in set theory to describe a NOT relationship. The notation for complement of set $A$ is $A'$. For example $A' = \text {NOT in set } A $.
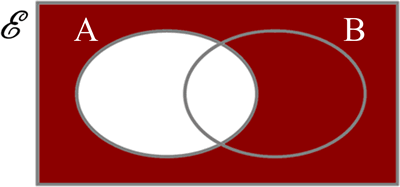
Set theory is the branch of logic which deals with collections of objects. These objects can be pretty much anything at all. A set is generally written as a description or a list of elements inside braces {}, eg. A={1, 2, 3}; Set $A$ contains the elements $1, 2$ and $3$. The language in which Set theory is expressed is called Boolean Algebra, which includes symbols such as Intersection $\cap$, Union $\cup$, Subset $\subset$, Membership $\in$
A Venn Diagrams are named after mathematician John Venn who extended the work of George Boole in logic and probability. Venn diagrams give a visual display of relationships between sets.